[FUTA, Akure] MTS 102: Introductory Mathematics II
2
Learning Track Courses
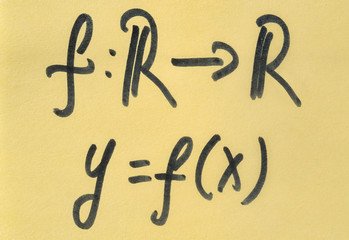 Single-Variable Functions and Their GraphsThis course introduces the basic concept of a function of a single real variable. It explores how such functions are represented algebraically and graphically, emphasizing interpretation and behavior on the real number line.
You’ll learn to identify domain, range, and key features of graphs such as intercepts, symmetry, and asymptotic behavior. The goal is to build a solid understanding of how functions behave visually and analytically.
This course sets the foundation for everything else in calculus. It is designed to be intuitive, but also precise in its treatment of core ideas.
Single-Variable Functions and Their GraphsThis course introduces the basic concept of a function of a single real variable. It explores how such functions are represented algebraically and graphically, emphasizing interpretation and behavior on the real number line.
You’ll learn to identify domain, range, and key features of graphs such as intercepts, symmetry, and asymptotic behavior. The goal is to build a solid understanding of how functions behave visually and analytically.
This course sets the foundation for everything else in calculus. It is designed to be intuitive, but also precise in its treatment of core ideas.
This course introduces the basic concept of a function of a single real variable. It explores how such functions are represented algebraically and graphically, emphasizing interpretation and behavior on the real number line. You’ll learn to identify domain, range, and key features of graphs such as intercepts, symmetry, and asymptotic behavior. The goal is to build a solid understanding of how functions behave visually and analytically. This course sets the foundation for everything else in calculus. It is designed to be intuitive, but also precise in its treatment of core ideas.
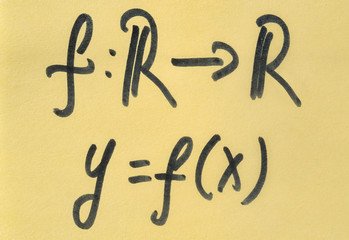 Limits of Functions — Single-Variable CalculusLimits form the conceptual entry point into calculus. This course focuses on the idea of approaching a value — what it means for a function to tend toward a limit, and how to analyze this behavior rigorously.
We examine left-hand and right-hand limits, infinite limits, and limits at infinity. You'll also learn to handle indeterminate forms and use algebraic techniques to simplify complex limit expressions.
By the end of the course, you’ll have a clear grasp of how limits underpin both continuity and derivatives, and why they matter.
Limits of Functions — Single-Variable CalculusLimits form the conceptual entry point into calculus. This course focuses on the idea of approaching a value — what it means for a function to tend toward a limit, and how to analyze this behavior rigorously.
We examine left-hand and right-hand limits, infinite limits, and limits at infinity. You'll also learn to handle indeterminate forms and use algebraic techniques to simplify complex limit expressions.
By the end of the course, you’ll have a clear grasp of how limits underpin both continuity and derivatives, and why they matter.
Limits form the conceptual entry point into calculus. This course focuses on the idea of approaching a value — what it means for a function to tend toward a limit, and how to analyze this behavior rigorously. We examine left-hand and right-hand limits, infinite limits, and limits at infinity. You'll also learn to handle indeterminate forms and use algebraic techniques to simplify complex limit expressions. By the end of the course, you’ll have a clear grasp of how limits underpin both continuity and derivatives, and why they matter.
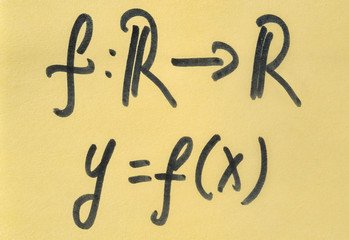 Continuity of Functions — Single-Variable CalculusThis course defines what it means for a function to be continuous at a point and on an interval. It connects the idea of a limit to the real-world expectation that a continuous function should have no breaks or jumps.
We go over types of discontinuities and how to classify them. You'll learn how to test for continuity using limit laws and understand the significance of continuity in applied contexts.
Continuity is a gateway concept that prepares you for more advanced ideas like differentiability and integrability.
Continuity of Functions — Single-Variable CalculusThis course defines what it means for a function to be continuous at a point and on an interval. It connects the idea of a limit to the real-world expectation that a continuous function should have no breaks or jumps.
We go over types of discontinuities and how to classify them. You'll learn how to test for continuity using limit laws and understand the significance of continuity in applied contexts.
Continuity is a gateway concept that prepares you for more advanced ideas like differentiability and integrability.
This course defines what it means for a function to be continuous at a point and on an interval. It connects the idea of a limit to the real-world expectation that a continuous function should have no breaks or jumps. We go over types of discontinuities and how to classify them. You'll learn how to test for continuity using limit laws and understand the significance of continuity in applied contexts. Continuity is a gateway concept that prepares you for more advanced ideas like differentiability and integrability.
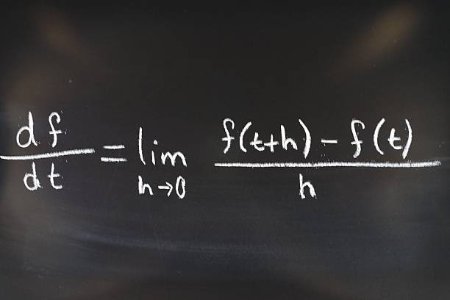 Differentiability and Derivatives of Functions — Single-Variable CalculusHere, you’ll learn what it means for a function to be differentiable and how to compute derivatives using first principles. We explore the derivative as a measure of instantaneous rate of change and as the slope of a tangent line.
The course also highlights the relationship between differentiability and continuity, and includes geometric and physical interpretations of the derivative.
This is where the core machinery of calculus really begins, with the derivative acting as a powerful tool for analysis.
Differentiability and Derivatives of Functions — Single-Variable CalculusHere, you’ll learn what it means for a function to be differentiable and how to compute derivatives using first principles. We explore the derivative as a measure of instantaneous rate of change and as the slope of a tangent line.
The course also highlights the relationship between differentiability and continuity, and includes geometric and physical interpretations of the derivative.
This is where the core machinery of calculus really begins, with the derivative acting as a powerful tool for analysis.
Here, you’ll learn what it means for a function to be differentiable and how to compute derivatives using first principles. We explore the derivative as a measure of instantaneous rate of change and as the slope of a tangent line. The course also highlights the relationship between differentiability and continuity, and includes geometric and physical interpretations of the derivative. This is where the core machinery of calculus really begins, with the derivative acting as a powerful tool for analysis.
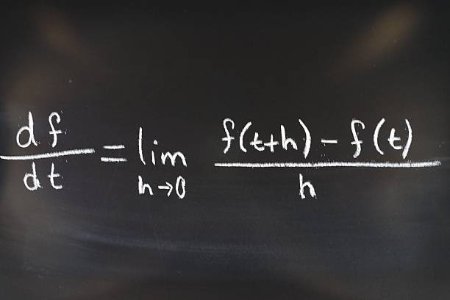 Techniques of Differentiation — Single-Variable CalculusThis course builds on your understanding of the derivative by introducing standard differentiation techniques. These include the product rule, quotient rule, and chain rule, as well as derivatives of polynomial, exponential, logarithmic, and trigonometric functions.
You’ll also learn to differentiate composite and implicit functions. The course emphasizes accuracy, pattern recognition, and methodical execution of differentiation steps.
It’s structured to ensure that by the end, finding derivatives becomes second nature.
Techniques of Differentiation — Single-Variable CalculusThis course builds on your understanding of the derivative by introducing standard differentiation techniques. These include the product rule, quotient rule, and chain rule, as well as derivatives of polynomial, exponential, logarithmic, and trigonometric functions.
You’ll also learn to differentiate composite and implicit functions. The course emphasizes accuracy, pattern recognition, and methodical execution of differentiation steps.
It’s structured to ensure that by the end, finding derivatives becomes second nature.
This course builds on your understanding of the derivative by introducing standard differentiation techniques. These include the product rule, quotient rule, and chain rule, as well as derivatives of polynomial, exponential, logarithmic, and trigonometric functions. You’ll also learn to differentiate composite and implicit functions. The course emphasizes accuracy, pattern recognition, and methodical execution of differentiation steps. It’s structured to ensure that by the end, finding derivatives becomes second nature.
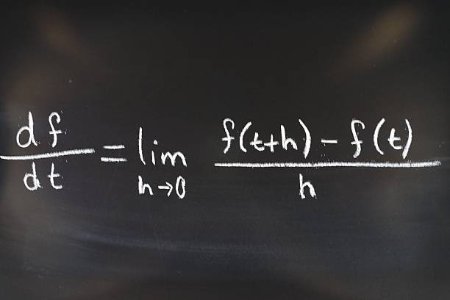 Applications of Differentiation — Single-Variable CalculusOnce you know how to differentiate, the next step is understanding what to do with the derivative. This course covers real-world applications, such as curve sketching, optimization, and motion problems.
We discuss how derivatives help find local extrema, inflection points, and intervals of increase or decrease. You'll also explore related rates and the Mean Value Theorem.
It’s a practical and insightful course that shows how calculus models change and solves tangible problems.
Applications of Differentiation — Single-Variable CalculusOnce you know how to differentiate, the next step is understanding what to do with the derivative. This course covers real-world applications, such as curve sketching, optimization, and motion problems.
We discuss how derivatives help find local extrema, inflection points, and intervals of increase or decrease. You'll also explore related rates and the Mean Value Theorem.
It’s a practical and insightful course that shows how calculus models change and solves tangible problems.
Once you know how to differentiate, the next step is understanding what to do with the derivative. This course covers real-world applications, such as curve sketching, optimization, and motion problems. We discuss how derivatives help find local extrema, inflection points, and intervals of increase or decrease. You'll also explore related rates and the Mean Value Theorem. It’s a practical and insightful course that shows how calculus models change and solves tangible problems.
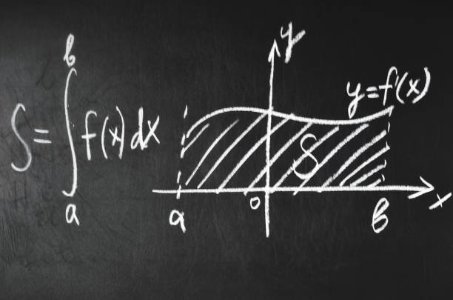 Anti-Derivatives — Single-Variable CalculusThis course introduces the idea of an anti-derivative — the inverse process of differentiation. You’ll learn how to find general and particular anti-derivatives of standard functions.
We focus on basic integration rules and how they relate directly to derivative patterns. This course also lays the groundwork for definite integrals and the Fundamental Theorem of Calculus.
It’s a gentle but critical step toward integral calculus.
Anti-Derivatives — Single-Variable CalculusThis course introduces the idea of an anti-derivative — the inverse process of differentiation. You’ll learn how to find general and particular anti-derivatives of standard functions.
We focus on basic integration rules and how they relate directly to derivative patterns. This course also lays the groundwork for definite integrals and the Fundamental Theorem of Calculus.
It’s a gentle but critical step toward integral calculus.
This course introduces the idea of an anti-derivative — the inverse process of differentiation. You’ll learn how to find general and particular anti-derivatives of standard functions. We focus on basic integration rules and how they relate directly to derivative patterns. This course also lays the groundwork for definite integrals and the Fundamental Theorem of Calculus. It’s a gentle but critical step toward integral calculus.
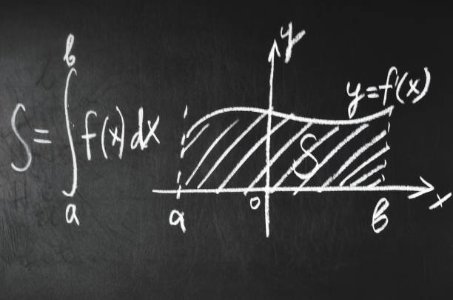 Techniques of Integration — Single-Variable CalculusWith the basics in place, this course moves into practical methods of integration, such as substitution, integration by parts, and partial fractions.
You’ll learn when and how to apply each technique, and how to recognize integrable forms efficiently. We also cover integrals involving trigonometric identities and improper integrals.
It’s a hands-on course that gives you the tools to handle a wide range of integral expressions confidently.
Techniques of Integration — Single-Variable CalculusWith the basics in place, this course moves into practical methods of integration, such as substitution, integration by parts, and partial fractions.
You’ll learn when and how to apply each technique, and how to recognize integrable forms efficiently. We also cover integrals involving trigonometric identities and improper integrals.
It’s a hands-on course that gives you the tools to handle a wide range of integral expressions confidently.
With the basics in place, this course moves into practical methods of integration, such as substitution, integration by parts, and partial fractions. You’ll learn when and how to apply each technique, and how to recognize integrable forms efficiently. We also cover integrals involving trigonometric identities and improper integrals. It’s a hands-on course that gives you the tools to handle a wide range of integral expressions confidently.
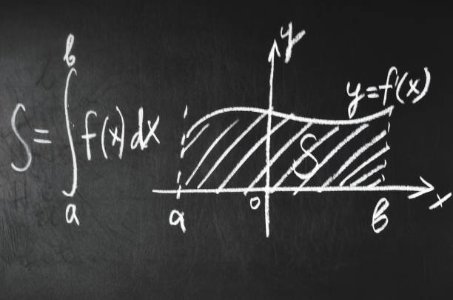 Applications of Integration — Single-Variable CalculusIn this final course of the track, you’ll apply integration to solve real problems: computing areas under curves, volumes of solids of revolution, and average values of functions.
We also examine applications in physics and engineering contexts, like displacement, work, and center of mass.
The course brings together all the skills you’ve built across the series and shows the power of calculus in understanding the physical world.
Applications of Integration — Single-Variable CalculusIn this final course of the track, you’ll apply integration to solve real problems: computing areas under curves, volumes of solids of revolution, and average values of functions.
We also examine applications in physics and engineering contexts, like displacement, work, and center of mass.
The course brings together all the skills you’ve built across the series and shows the power of calculus in understanding the physical world.
In this final course of the track, you’ll apply integration to solve real problems: computing areas under curves, volumes of solids of revolution, and average values of functions. We also examine applications in physics and engineering contexts, like displacement, work, and center of mass. The course brings together all the skills you’ve built across the series and shows the power of calculus in understanding the physical world.