[UNILAG, Akoka] MTH 102: Elementary Mathematics II
Learning Track Courses
 Functions and Their Graphs - Single-Variable Calculus (Undergraduate Foundation)This course provides a rigorous foundation in the concept of functions, the building block of calculus. We begin with the real number system - rationals, irrationals, intervals, and infinity - before defining real-valued functions, their domains, and ranges. You will systematically study all key function families: polynomial, rational, algebraic, piecewise-defined, and transcendental, including exponential, logarithmic, trigonometric, and hyperbolic types.
A command of functions is essential for all technical and quantitative disciplines. These principles are directly applied in physics to model motion, in economics for supply-demand curves, in engineering for signal processing, and in computer science to analyse algorithm complexity. This course delivers the core mathematical tools required for effective modelling and problem-solving in these fields and beyond.
By the end of this course, you will be able to: calculate the domain and range of any given function; classify functions and identify their fundamental properties; analyse functions for key characteristics like symmetry (odd and even); and accurately construct graphs for a wide range of standard and piecewise-defined functions directly from their equations.
This course is designed for first-year undergraduates in science, technology, engineering, mathematics (STEM), and economics. It is also critical for any student preparing for advanced calculus or for professionals who require a solid mathematical base for roles in finance, data science, or technical research.
Functions and Their Graphs - Single-Variable Calculus (Undergraduate Foundation)This course provides a rigorous foundation in the concept of functions, the building block of calculus. We begin with the real number system - rationals, irrationals, intervals, and infinity - before defining real-valued functions, their domains, and ranges. You will systematically study all key function families: polynomial, rational, algebraic, piecewise-defined, and transcendental, including exponential, logarithmic, trigonometric, and hyperbolic types.
A command of functions is essential for all technical and quantitative disciplines. These principles are directly applied in physics to model motion, in economics for supply-demand curves, in engineering for signal processing, and in computer science to analyse algorithm complexity. This course delivers the core mathematical tools required for effective modelling and problem-solving in these fields and beyond.
By the end of this course, you will be able to: calculate the domain and range of any given function; classify functions and identify their fundamental properties; analyse functions for key characteristics like symmetry (odd and even); and accurately construct graphs for a wide range of standard and piecewise-defined functions directly from their equations.
This course is designed for first-year undergraduates in science, technology, engineering, mathematics (STEM), and economics. It is also critical for any student preparing for advanced calculus or for professionals who require a solid mathematical base for roles in finance, data science, or technical research.
This course provides a rigorous foundation in the concept of functions, the building block of calculus. We begin with the real number system - rationals, irrationals, intervals, and infinity - before defining real-valued functions, their domains, and ranges. You will systematically study all key function families: polynomial, rational, algebraic, piecewise-defined, and transcendental, including exponential, logarithmic, trigonometric, and hyperbolic types. A command of functions is essential for all technical and quantitative disciplines. These principles are directly applied in physics to model motion, in economics for supply-demand curves, in engineering for signal processing, and in computer science to analyse algorithm complexity. This course delivers the core mathematical tools required for effective modelling and problem-solving in these fields and beyond. By the end of this course, you will be able to: calculate the domain and range of any given function; classify functions and identify their fundamental properties; analyse functions for key characteristics like symmetry (odd and even); and accurately construct graphs for a wide range of standard and piecewise-defined functions directly from their equations. This course is designed for first-year undergraduates in science, technology, engineering, mathematics (STEM), and economics. It is also critical for any student preparing for advanced calculus or for professionals who require a solid mathematical base for roles in finance, data science, or technical research.
 Limits of Functions - Single-Variable Calculus (Undergraduate Foundation)This course provides a rigorous introduction to the concept of the limit, the theoretical bedrock upon which all of calculus is built. We will move from an intuitive understanding of what it means for a function to 'approach' a value to the algebraic techniques required for precise evaluation. The course covers the limit laws, methods for handling indeterminate forms, and the behavior of functions at infinity.
Understanding limits is non-negotiable for any serious study of calculus. The principles developed here are not merely abstract; they are the tools used to formally define the core concepts of calculus that are used to model the mechanics of change that govern engineering, physics, economics, and computer science.
By the end of this course, you will be able to: evaluate limits graphically, numerically, and algebraically; apply the Squeeze Theorem and L’Hôpital’s Rule; analyse the end-behavior of functions; and identify vertical and horizontal asymptotes.
This course is designed for first-year undergraduates in STEM fields who are beginning their calculus sequence. It is an essential prerequisite for subsequent courses on continuity and differentiability and is also invaluable for any student or professional seeking to rebuild their mathematical foundation from first principles.
Limits of Functions - Single-Variable Calculus (Undergraduate Foundation)This course provides a rigorous introduction to the concept of the limit, the theoretical bedrock upon which all of calculus is built. We will move from an intuitive understanding of what it means for a function to 'approach' a value to the algebraic techniques required for precise evaluation. The course covers the limit laws, methods for handling indeterminate forms, and the behavior of functions at infinity.
Understanding limits is non-negotiable for any serious study of calculus. The principles developed here are not merely abstract; they are the tools used to formally define the core concepts of calculus that are used to model the mechanics of change that govern engineering, physics, economics, and computer science.
By the end of this course, you will be able to: evaluate limits graphically, numerically, and algebraically; apply the Squeeze Theorem and L’Hôpital’s Rule; analyse the end-behavior of functions; and identify vertical and horizontal asymptotes.
This course is designed for first-year undergraduates in STEM fields who are beginning their calculus sequence. It is an essential prerequisite for subsequent courses on continuity and differentiability and is also invaluable for any student or professional seeking to rebuild their mathematical foundation from first principles.
This course provides a rigorous introduction to the concept of the limit, the theoretical bedrock upon which all of calculus is built. We will move from an intuitive understanding of what it means for a function to 'approach' a value to the algebraic techniques required for precise evaluation. The course covers the limit laws, methods for handling indeterminate forms, and the behavior of functions at infinity. Understanding limits is non-negotiable for any serious study of calculus. The principles developed here are not merely abstract; they are the tools used to formally define the core concepts of calculus that are used to model the mechanics of change that govern engineering, physics, economics, and computer science. By the end of this course, you will be able to: evaluate limits graphically, numerically, and algebraically; apply the Squeeze Theorem and L’Hôpital’s Rule; analyse the end-behavior of functions; and identify vertical and horizontal asymptotes. This course is designed for first-year undergraduates in STEM fields who are beginning their calculus sequence. It is an essential prerequisite for subsequent courses on continuity and differentiability and is also invaluable for any student or professional seeking to rebuild their mathematical foundation from first principles.
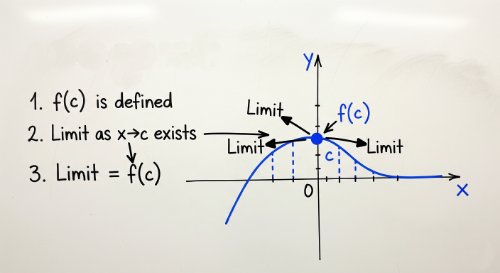 Continuity of Functions - Single-Variable Calculus (Undergraduate Foundation)This course provides a focused and rigorous examination of continuity, a fundamental property of functions that underpins the whole of differential and integral calculus. We move from an intuitive understanding of "unbroken" graphs to the formal, limit-based definition of continuity. The course systematically explores the different types of discontinuities and the powerful theorems that apply only to continuous functions.
A command of continuity is essential for understanding why calculus works. This concept ensures that functions are predictable and well-behaved, a necessary condition for modeling real-world phenomena and for the validity of the major theorems of calculus. It is the bridge between the concept of a limit and the concept of a derivative, explaining why a function must be continuous to be differentiable.
By the end of this course, you will be able to use the three-part definition to test for continuity at a point, identify and classify removable, jump, and infinite discontinuities, and apply the Intermediate Value Theorem and the Extreme Value Theorem to analyse function behavior on a closed interval.
This course is designed for first-year undergraduates in science, technology, engineering, and mathematics who have completed a course on limits. It is a critical prerequisite for the study of differentiability and is essential for any student seeking a deep understanding of calculus theory.
Continuity of Functions - Single-Variable Calculus (Undergraduate Foundation)This course provides a focused and rigorous examination of continuity, a fundamental property of functions that underpins the whole of differential and integral calculus. We move from an intuitive understanding of "unbroken" graphs to the formal, limit-based definition of continuity. The course systematically explores the different types of discontinuities and the powerful theorems that apply only to continuous functions.
A command of continuity is essential for understanding why calculus works. This concept ensures that functions are predictable and well-behaved, a necessary condition for modeling real-world phenomena and for the validity of the major theorems of calculus. It is the bridge between the concept of a limit and the concept of a derivative, explaining why a function must be continuous to be differentiable.
By the end of this course, you will be able to use the three-part definition to test for continuity at a point, identify and classify removable, jump, and infinite discontinuities, and apply the Intermediate Value Theorem and the Extreme Value Theorem to analyse function behavior on a closed interval.
This course is designed for first-year undergraduates in science, technology, engineering, and mathematics who have completed a course on limits. It is a critical prerequisite for the study of differentiability and is essential for any student seeking a deep understanding of calculus theory.
This course provides a focused and rigorous examination of continuity, a fundamental property of functions that underpins the whole of differential and integral calculus. We move from an intuitive understanding of "unbroken" graphs to the formal, limit-based definition of continuity. The course systematically explores the different types of discontinuities and the powerful theorems that apply only to continuous functions. A command of continuity is essential for understanding why calculus works. This concept ensures that functions are predictable and well-behaved, a necessary condition for modeling real-world phenomena and for the validity of the major theorems of calculus. It is the bridge between the concept of a limit and the concept of a derivative, explaining why a function must be continuous to be differentiable. By the end of this course, you will be able to use the three-part definition to test for continuity at a point, identify and classify removable, jump, and infinite discontinuities, and apply the Intermediate Value Theorem and the Extreme Value Theorem to analyse function behavior on a closed interval. This course is designed for first-year undergraduates in science, technology, engineering, and mathematics who have completed a course on limits. It is a critical prerequisite for the study of differentiability and is essential for any student seeking a deep understanding of calculus theory.
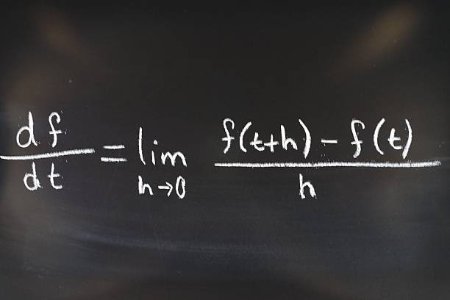 Differentiability of Functions - Single-Variable Calculus (Undergraduate Foundation)This course provides a rigorous, theoretical introduction to differential calculus. We will move beyond computation to understand the fundamental nature of the derivative, beginning with its formal definition as the limit of a difference quotient. The curriculum is designed to build a deep conceptual understanding of what it means for a function to be differentiable and the profound consequences of this property.
The primary focus is on formal proofs and theoretical results. We will systematically derive the rules of differentiation, including the product, quotient, and chain rules, directly from first principles. This course emphasizes the "why" behind the mechanics of calculus, establishing the logical framework upon which all applications are built, including the cornerstone theorems of Rolle, the Mean Value Theorem, and Taylor's Theorem.
By the end of this course, you will be able to: explain the derivative from its limit definition; prove the relationship between differentiability and continuity; formally derive all major differentiation rules; and understand the theoretical significance of the Mean Value Theorem and Taylor's Theorem.
This course is designed for first-year undergraduates in mathematics, physics, and engineering who require a deep theoretical foundation for their studies. It is the ideal precursor to subsequent courses on differentiation techniques and applications, providing the essential logical underpinnings for those more practical subjects.
Differentiability of Functions - Single-Variable Calculus (Undergraduate Foundation)This course provides a rigorous, theoretical introduction to differential calculus. We will move beyond computation to understand the fundamental nature of the derivative, beginning with its formal definition as the limit of a difference quotient. The curriculum is designed to build a deep conceptual understanding of what it means for a function to be differentiable and the profound consequences of this property.
The primary focus is on formal proofs and theoretical results. We will systematically derive the rules of differentiation, including the product, quotient, and chain rules, directly from first principles. This course emphasizes the "why" behind the mechanics of calculus, establishing the logical framework upon which all applications are built, including the cornerstone theorems of Rolle, the Mean Value Theorem, and Taylor's Theorem.
By the end of this course, you will be able to: explain the derivative from its limit definition; prove the relationship between differentiability and continuity; formally derive all major differentiation rules; and understand the theoretical significance of the Mean Value Theorem and Taylor's Theorem.
This course is designed for first-year undergraduates in mathematics, physics, and engineering who require a deep theoretical foundation for their studies. It is the ideal precursor to subsequent courses on differentiation techniques and applications, providing the essential logical underpinnings for those more practical subjects.
This course provides a rigorous, theoretical introduction to differential calculus. We will move beyond computation to understand the fundamental nature of the derivative, beginning with its formal definition as the limit of a difference quotient. The curriculum is designed to build a deep conceptual understanding of what it means for a function to be differentiable and the profound consequences of this property. The primary focus is on formal proofs and theoretical results. We will systematically derive the rules of differentiation, including the product, quotient, and chain rules, directly from first principles. This course emphasizes the "why" behind the mechanics of calculus, establishing the logical framework upon which all applications are built, including the cornerstone theorems of Rolle, the Mean Value Theorem, and Taylor's Theorem. By the end of this course, you will be able to: explain the derivative from its limit definition; prove the relationship between differentiability and continuity; formally derive all major differentiation rules; and understand the theoretical significance of the Mean Value Theorem and Taylor's Theorem. This course is designed for first-year undergraduates in mathematics, physics, and engineering who require a deep theoretical foundation for their studies. It is the ideal precursor to subsequent courses on differentiation techniques and applications, providing the essential logical underpinnings for those more practical subjects.
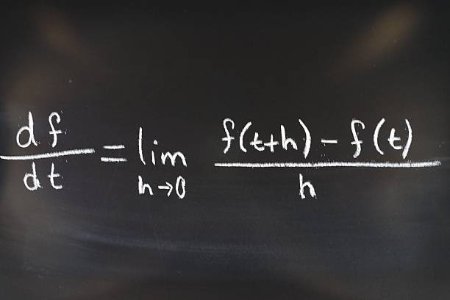 Techniques of Differentiation - Single-Variable Calculus (Undergraduate Foundation)This course builds on your understanding of the derivative by introducing standard differentiation techniques. These include the product rule, quotient rule, and chain rule, as well as derivatives of polynomial, exponential, logarithmic, and trigonometric functions.
You’ll also learn to differentiate composite and implicit functions. The course emphasizes accuracy, pattern recognition, and methodical execution of differentiation steps.
It’s structured to ensure that by the end, finding derivatives becomes second nature.
Techniques of Differentiation - Single-Variable Calculus (Undergraduate Foundation)This course builds on your understanding of the derivative by introducing standard differentiation techniques. These include the product rule, quotient rule, and chain rule, as well as derivatives of polynomial, exponential, logarithmic, and trigonometric functions.
You’ll also learn to differentiate composite and implicit functions. The course emphasizes accuracy, pattern recognition, and methodical execution of differentiation steps.
It’s structured to ensure that by the end, finding derivatives becomes second nature.
This course builds on your understanding of the derivative by introducing standard differentiation techniques. These include the product rule, quotient rule, and chain rule, as well as derivatives of polynomial, exponential, logarithmic, and trigonometric functions. You’ll also learn to differentiate composite and implicit functions. The course emphasizes accuracy, pattern recognition, and methodical execution of differentiation steps. It’s structured to ensure that by the end, finding derivatives becomes second nature.
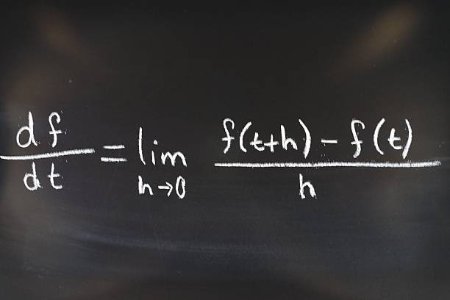 Applications of Differentiation - Single-Variable Calculus (Undergraduate Foundation)Once you know how to differentiate, the next step is understanding what to do with the derivative. This course covers real-world applications, such as curve sketching, optimization, and motion problems.
We discuss how derivatives help find local extrema, inflection points, and intervals of increase or decrease. You'll also explore related rates and the Mean Value Theorem.
It’s a practical and insightful course that shows how calculus models change and solves tangible problems.
Applications of Differentiation - Single-Variable Calculus (Undergraduate Foundation)Once you know how to differentiate, the next step is understanding what to do with the derivative. This course covers real-world applications, such as curve sketching, optimization, and motion problems.
We discuss how derivatives help find local extrema, inflection points, and intervals of increase or decrease. You'll also explore related rates and the Mean Value Theorem.
It’s a practical and insightful course that shows how calculus models change and solves tangible problems.
Once you know how to differentiate, the next step is understanding what to do with the derivative. This course covers real-world applications, such as curve sketching, optimization, and motion problems. We discuss how derivatives help find local extrema, inflection points, and intervals of increase or decrease. You'll also explore related rates and the Mean Value Theorem. It’s a practical and insightful course that shows how calculus models change and solves tangible problems.
 Anti-Derivatives - Single-Variable Calculus (Undergraduate Foundation)This course introduces the idea of an anti-derivative — the inverse process of differentiation. You’ll learn how to find general and particular anti-derivatives of standard functions.
We focus on basic integration rules and how they relate directly to derivative patterns. This course also lays the groundwork for definite integrals and the Fundamental Theorem of Calculus.
It’s a gentle but critical step toward integral calculus.
Anti-Derivatives - Single-Variable Calculus (Undergraduate Foundation)This course introduces the idea of an anti-derivative — the inverse process of differentiation. You’ll learn how to find general and particular anti-derivatives of standard functions.
We focus on basic integration rules and how they relate directly to derivative patterns. This course also lays the groundwork for definite integrals and the Fundamental Theorem of Calculus.
It’s a gentle but critical step toward integral calculus.
This course introduces the idea of an anti-derivative — the inverse process of differentiation. You’ll learn how to find general and particular anti-derivatives of standard functions. We focus on basic integration rules and how they relate directly to derivative patterns. This course also lays the groundwork for definite integrals and the Fundamental Theorem of Calculus. It’s a gentle but critical step toward integral calculus.
 Techniques of Integration - Single-Variable Calculus (Undergraduate Foundation)With the basics in place, this course moves into practical methods of integration, such as substitution, integration by parts, and partial fractions.
You’ll learn when and how to apply each technique, and how to recognize integrable forms efficiently. We also cover integrals involving trigonometric identities and improper integrals.
It’s a hands-on course that gives you the tools to handle a wide range of integral expressions confidently.
Techniques of Integration - Single-Variable Calculus (Undergraduate Foundation)With the basics in place, this course moves into practical methods of integration, such as substitution, integration by parts, and partial fractions.
You’ll learn when and how to apply each technique, and how to recognize integrable forms efficiently. We also cover integrals involving trigonometric identities and improper integrals.
It’s a hands-on course that gives you the tools to handle a wide range of integral expressions confidently.
With the basics in place, this course moves into practical methods of integration, such as substitution, integration by parts, and partial fractions. You’ll learn when and how to apply each technique, and how to recognize integrable forms efficiently. We also cover integrals involving trigonometric identities and improper integrals. It’s a hands-on course that gives you the tools to handle a wide range of integral expressions confidently.
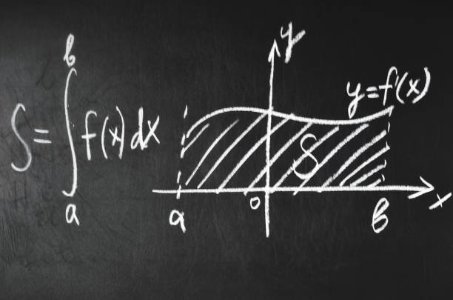
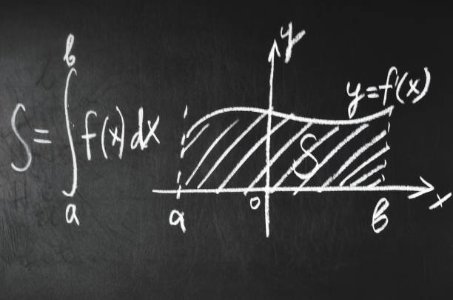
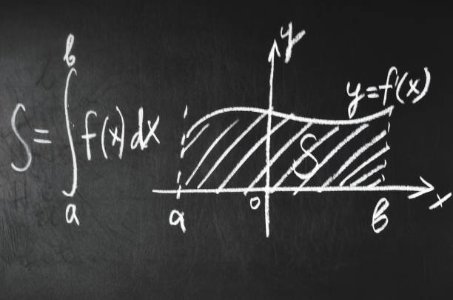 Applications of Integration - Single-Variable Calculus (Undergraduate Foundation)In this final course of the track, you’ll apply integration to solve real problems: computing areas under curves, volumes of solids of revolution, and average values of functions.
We also examine applications in physics and engineering contexts, like displacement, work, and center of mass.
The course brings together all the skills you’ve built across the series and shows the power of calculus in understanding the physical world.
Applications of Integration - Single-Variable Calculus (Undergraduate Foundation)In this final course of the track, you’ll apply integration to solve real problems: computing areas under curves, volumes of solids of revolution, and average values of functions.
We also examine applications in physics and engineering contexts, like displacement, work, and center of mass.
The course brings together all the skills you’ve built across the series and shows the power of calculus in understanding the physical world.
In this final course of the track, you’ll apply integration to solve real problems: computing areas under curves, volumes of solids of revolution, and average values of functions. We also examine applications in physics and engineering contexts, like displacement, work, and center of mass. The course brings together all the skills you’ve built across the series and shows the power of calculus in understanding the physical world.
 Introduction to Numerical Methods (Undergraduate Foundation)This course covers numerical methods for solving problems that have no exact analytical solution. It is a practical study of iterative approximation techniques. The material is focused on two core areas: finding the roots of single-variable equations using the Bisection and Newton's methods, and approximating definite integrals using the Trapezoidal and Simpson's rules.
Numerical methods are the foundation of all modern computational problem-solving in science, engineering, and finance. These are the algorithms that power computer simulations, engineering design software, and financial modelling tools. The ability to find approximate solutions to complex equations is a fundamental skill for any technical or scientific professional.
By the end of this course, you will be able to apply the Bisection and Newton's methods to find the roots of single-variable equations. You will also be able to use the Trapezoidal and Simpson's rules to calculate the approximate value of definite integrals, providing a core toolkit for numerical approximation.
This course is for undergraduate foundation students in engineering, physics, and computer science. It is an essential topic for anyone who will use computational tools to solve mathematical problems. A solid understanding of single-variable calculus is a prerequisite.
Introduction to Numerical Methods (Undergraduate Foundation)This course covers numerical methods for solving problems that have no exact analytical solution. It is a practical study of iterative approximation techniques. The material is focused on two core areas: finding the roots of single-variable equations using the Bisection and Newton's methods, and approximating definite integrals using the Trapezoidal and Simpson's rules.
Numerical methods are the foundation of all modern computational problem-solving in science, engineering, and finance. These are the algorithms that power computer simulations, engineering design software, and financial modelling tools. The ability to find approximate solutions to complex equations is a fundamental skill for any technical or scientific professional.
By the end of this course, you will be able to apply the Bisection and Newton's methods to find the roots of single-variable equations. You will also be able to use the Trapezoidal and Simpson's rules to calculate the approximate value of definite integrals, providing a core toolkit for numerical approximation.
This course is for undergraduate foundation students in engineering, physics, and computer science. It is an essential topic for anyone who will use computational tools to solve mathematical problems. A solid understanding of single-variable calculus is a prerequisite.
This course covers numerical methods for solving problems that have no exact analytical solution. It is a practical study of iterative approximation techniques. The material is focused on two core areas: finding the roots of single-variable equations using the Bisection and Newton's methods, and approximating definite integrals using the Trapezoidal and Simpson's rules. Numerical methods are the foundation of all modern computational problem-solving in science, engineering, and finance. These are the algorithms that power computer simulations, engineering design software, and financial modelling tools. The ability to find approximate solutions to complex equations is a fundamental skill for any technical or scientific professional. By the end of this course, you will be able to apply the Bisection and Newton's methods to find the roots of single-variable equations. You will also be able to use the Trapezoidal and Simpson's rules to calculate the approximate value of definite integrals, providing a core toolkit for numerical approximation. This course is for undergraduate foundation students in engineering, physics, and computer science. It is an essential topic for anyone who will use computational tools to solve mathematical problems. A solid understanding of single-variable calculus is a prerequisite.