MTH 201: Mathematical Methods I
Learning Track Courses
Functions and Their Graphs - Single-Variable Calculus (Undergraduate Foundation)
This course provides a rigorous foundation in the concept of functions, the building block of calculus. We begin with the real number system - rationals, irrationals, intervals, and infinity - before defining real-valued functions, their domains, and ranges. You will systematically study all key function families: polynomial, rational, algebraic, piecewise-defined, and transcendental, including exponential, logarithmic, trigonometric, and hyperbolic types.
A command of functions is essential for all technical and quantitative disciplines. These principles are directly applied in physics to model motion, in economics for supply-demand curves, in engineering for signal processing, and in computer science to analyse algorithm complexity. This course delivers the core mathematical tools required for effective modelling and problem-solving in these fields and beyond.
By the end of this course, you will be able to: calculate the domain and range of any given function; classify functions and identify their fundamental properties; analyse functions for key characteristics like symmetry (odd and even); and accurately construct graphs for a wide range of standard and piecewise-defined functions directly from their equations.
This course is designed for first-year undergraduates in science, technology, engineering, mathematics (STEM), and economics. It is also critical for any student preparing for advanced calculus or for professionals who require a solid mathematical base for roles in finance, data science, or technical research.
Functions and Their Graphs - Single-Variable Calculus (Undergraduate Foundation)
This course provides a rigorous foundation in the concept of functions, the building block of calculus. We begin with the real number system - rationals, irrationals, intervals, and infinity - before defining real-valued functions, their domains, and ranges. You will systematically study all key function families: polynomial, rational, algebraic, piecewise-defined, and transcendental, including exponential, logarithmic, trigonometric, and hyperbolic types. A command of functions is essential for all technical and quantitative disciplines. These principles are directly applied in physics to model motion, in economics for supply-demand curves, in engineering for signal processing, and in computer science to analyse algorithm complexity. This course delivers the core mathematical tools required for effective modelling and problem-solving in these fields and beyond. By the end of this course, you will be able to: calculate the domain and range of any given function; classify functions and identify their fundamental properties; analyse functions for key characteristics like symmetry (odd and even); and accurately construct graphs for a wide range of standard and piecewise-defined functions directly from their equations. This course is designed for first-year undergraduates in science, technology, engineering, mathematics (STEM), and economics. It is also critical for any student preparing for advanced calculus or for professionals who require a solid mathematical base for roles in finance, data science, or technical research.
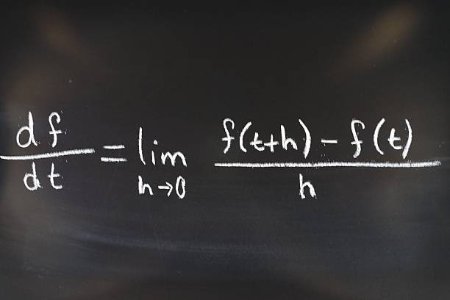
Differentiability of Functions - Single-Variable Calculus (Undergraduate Foundation)
This course provides a rigorous, theoretical introduction to differential calculus. We will move beyond computation to understand the fundamental nature of the derivative, beginning with its formal definition as the limit of a difference quotient. The curriculum is designed to build a deep conceptual understanding of what it means for a function to be differentiable and the profound consequences of this property.
The primary focus is on formal proofs and theoretical results. We will systematically derive the rules of differentiation, including the product, quotient, and chain rules, directly from first principles. This course emphasizes the "why" behind the mechanics of calculus, establishing the logical framework upon which all applications are built, including the cornerstone theorems of Rolle, the Mean Value Theorem, and Taylor's Theorem.
By the end of this course, you will be able to: explain the derivative from its limit definition; prove the relationship between differentiability and continuity; formally derive all major differentiation rules; and understand the theoretical significance of the Mean Value Theorem and Taylor's Theorem.
This course is designed for first-year undergraduates in mathematics, physics, and engineering who require a deep theoretical foundation for their studies. It is the ideal precursor to subsequent courses on differentiation techniques and applications, providing the essential logical underpinnings for those more practical subjects.
Differentiability of Functions - Single-Variable Calculus (Undergraduate Foundation)
This course provides a rigorous, theoretical introduction to differential calculus. We will move beyond computation to understand the fundamental nature of the derivative, beginning with its formal definition as the limit of a difference quotient. The curriculum is designed to build a deep conceptual understanding of what it means for a function to be differentiable and the profound consequences of this property. The primary focus is on formal proofs and theoretical results. We will systematically derive the rules of differentiation, including the product, quotient, and chain rules, directly from first principles. This course emphasizes the "why" behind the mechanics of calculus, establishing the logical framework upon which all applications are built, including the cornerstone theorems of Rolle, the Mean Value Theorem, and Taylor's Theorem. By the end of this course, you will be able to: explain the derivative from its limit definition; prove the relationship between differentiability and continuity; formally derive all major differentiation rules; and understand the theoretical significance of the Mean Value Theorem and Taylor's Theorem. This course is designed for first-year undergraduates in mathematics, physics, and engineering who require a deep theoretical foundation for their studies. It is the ideal precursor to subsequent courses on differentiation techniques and applications, providing the essential logical underpinnings for those more practical subjects.
Partial Differentiation and Its Applications - Multivariable Calculus (Undergraduate Advanced)
This course provides a complete guide to the calculus of several variables. It builds from the foundational concepts of multivariable functions, limits, and continuity to the core techniques of differentiation, including partial derivatives, the chain rule, and implicit differentiation. The material culminates in advanced topics such as Taylor's theorem for several variables and the use of Jacobians.
Multivariable calculus is the language of modern science, engineering, and economics. Its principles are used to model complex surfaces, analyse thermodynamic systems, create 3D computer graphics, and solve critical optimisation problems in business and finance. This is the mathematical toolkit for working with systems that have multiple interacting variables.
By the end of this course, you will be able to calculate partial derivatives, apply the multivariable chain rule, and find directional derivatives using the gradient vector. You will also be able to solve both unconstrained and constrained optimisation problems by finding extreme values and using the method of Lagrange multipliers, and apply these derivatives to find tangent planes to surfaces.
This course is for students who have completed a full single-variable calculus sequence. It is the standard curriculum for a multivariable calculus (Calculus III) module and is a direct prerequisite for the study of vector calculus, differential equations, and advanced courses in physics, engineering, and economics.
Partial Differentiation and Its Applications - Multivariable Calculus (Undergraduate Advanced)
This course provides a complete guide to the calculus of several variables. It builds from the foundational concepts of multivariable functions, limits, and continuity to the core techniques of differentiation, including partial derivatives, the chain rule, and implicit differentiation. The material culminates in advanced topics such as Taylor's theorem for several variables and the use of Jacobians. Multivariable calculus is the language of modern science, engineering, and economics. Its principles are used to model complex surfaces, analyse thermodynamic systems, create 3D computer graphics, and solve critical optimisation problems in business and finance. This is the mathematical toolkit for working with systems that have multiple interacting variables. By the end of this course, you will be able to calculate partial derivatives, apply the multivariable chain rule, and find directional derivatives using the gradient vector. You will also be able to solve both unconstrained and constrained optimisation problems by finding extreme values and using the method of Lagrange multipliers, and apply these derivatives to find tangent planes to surfaces. This course is for students who have completed a full single-variable calculus sequence. It is the standard curriculum for a multivariable calculus (Calculus III) module and is a direct prerequisite for the study of vector calculus, differential equations, and advanced courses in physics, engineering, and economics.