PHY 101: General Physics I - Mechanics
Learning Track Courses

Introduction to Physics (Undergraduate Foundation)
Physics is not a collection of facts; it is a quantitative language. This course establishes that language. We cover the formal system of measurement and units, the rigorous method of dimensional analysis, the complete framework of vector algebra, and the use of calculus to describe how vector quantities change. This is the essential grammar of science.
The tools in this course have immediate, practical applications. Correct dimensional analysis is a critical technique for verifying equations and preventing catastrophic errors in any technical calculation. Vectors are the required language for describing forces, displacements, velocities, and fields in any engineering or scientific discipline. Mastering this material is the first step to becoming a competent technical professional.
Upon completion, you will command the mathematical toolkit for physics. You will perform dimensional analysis to validate equations. You will resolve vectors into components, calculate vector sums and products, and differentiate vector functions to analyse rates of change, such as deriving velocity from a position vector.
This course is the mandatory starting point for first-year university students of engineering, physics, computer science, and related disciplines. A firm command of secondary school algebra, geometry, and trigonometry is a prerequisite. It is also suitable for professionals who require a rigorous and efficient refresher on the foundational mathematical tools of science.
Introduction to Physics (Undergraduate Foundation)
Physics is not a collection of facts; it is a quantitative language. This course establishes that language. We cover the formal system of measurement and units, the rigorous method of dimensional analysis, the complete framework of vector algebra, and the use of calculus to describe how vector quantities change. This is the essential grammar of science. The tools in this course have immediate, practical applications. Correct dimensional analysis is a critical technique for verifying equations and preventing catastrophic errors in any technical calculation. Vectors are the required language for describing forces, displacements, velocities, and fields in any engineering or scientific discipline. Mastering this material is the first step to becoming a competent technical professional. Upon completion, you will command the mathematical toolkit for physics. You will perform dimensional analysis to validate equations. You will resolve vectors into components, calculate vector sums and products, and differentiate vector functions to analyse rates of change, such as deriving velocity from a position vector. This course is the mandatory starting point for first-year university students of engineering, physics, computer science, and related disciplines. A firm command of secondary school algebra, geometry, and trigonometry is a prerequisite. It is also suitable for professionals who require a rigorous and efficient refresher on the foundational mathematical tools of science.
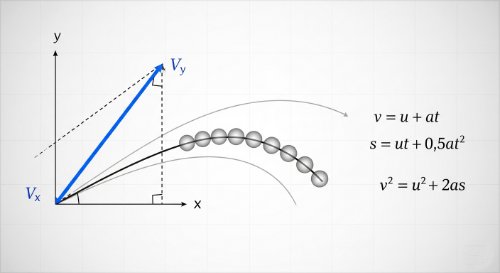
Kinematics: Motion in One and Two Dimensions - Physics (Undergraduate Foundation)
Motion is the most fundamental concept in physics. This course provides the mathematical framework to describe it with quantitative precision. We will systematically analyse motion in one, two, and three dimensions, progressing from motion along a straight line to the vector analysis of projectiles and general spatial motion. This requires a full command of both vector algebra and introductory calculus.
The principles of kinematics are the bedrock of physical analysis, engineering design, and biomechanics. This knowledge is required to analyse everything from vehicle performance and projectile trajectories to the movement of organisms and robotic motion. A command of this material is essential for any work involving the dynamics of moving systems, providing the tools to predict and control motion in the real world.
Upon completion, you will be able to analyse motion in multiple dimensions. You will solve one-dimensional problems using the standard kinematic equations for constant acceleration. You will analyse two-dimensional projectile motion by resolving vectors into independent components. Critically, you will use vector calculus to describe the general case of motion with variable acceleration.
This course is designed for first-year university students of the physical, biological, and medical sciences, as well as engineering and computer science. A firm command of vector algebra and introductory calculus (differentiation and integration) is a mandatory prerequisite. This material is the necessary foundation for the subsequent study of Newtonian dynamics and biomechanics.
Kinematics: Motion in One and Two Dimensions - Physics (Undergraduate Foundation)
Motion is the most fundamental concept in physics. This course provides the mathematical framework to describe it with quantitative precision. We will systematically analyse motion in one, two, and three dimensions, progressing from motion along a straight line to the vector analysis of projectiles and general spatial motion. This requires a full command of both vector algebra and introductory calculus. The principles of kinematics are the bedrock of physical analysis, engineering design, and biomechanics. This knowledge is required to analyse everything from vehicle performance and projectile trajectories to the movement of organisms and robotic motion. A command of this material is essential for any work involving the dynamics of moving systems, providing the tools to predict and control motion in the real world. Upon completion, you will be able to analyse motion in multiple dimensions. You will solve one-dimensional problems using the standard kinematic equations for constant acceleration. You will analyse two-dimensional projectile motion by resolving vectors into independent components. Critically, you will use vector calculus to describe the general case of motion with variable acceleration. This course is designed for first-year university students of the physical, biological, and medical sciences, as well as engineering and computer science. A firm command of vector algebra and introductory calculus (differentiation and integration) is a mandatory prerequisite. This material is the necessary foundation for the subsequent study of Newtonian dynamics and biomechanics.
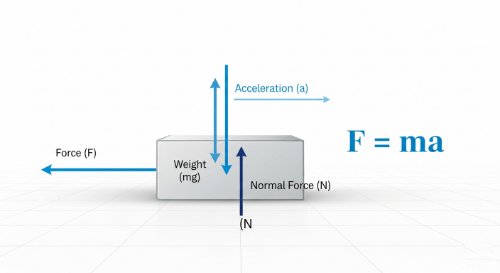
Force and Motion: Newton's Laws - Physics (Undergraduate Foundation)
Dynamics is the study of why objects move, and Newton's laws of motion provide the definitive mathematical framework for this analysis. This course transitions from kinematics to the rigorous application of force vectors, covering inertia, the quantitative relationship of mass and acceleration, and the necessity of action-reaction pairs. You will master the mechanics of special forces including gravity, tension, and springs, while resolving complex resistive interactions across static, kinetic, and fluid friction regimes.
Every mechanical system - from civil engineering structures to aerospace propulsion - operates under these foundational principles. Understanding the interaction of forces is essential for predicting system failure, calculating vehicular safety margins, and designing efficient machinery. This knowledge provides the analytical tools required to solve real-world problems involving particle equilibrium and dynamic acceleration in both linear and circular paths.
By the end of this course, you will be able to construct precise free-body diagrams to isolate bodies from their surroundings. You will acquire the technical skill to apply the second law to multi-force systems, calculate centripetal force requirements for uniform circular motion, and utilise the laws of equilibrium to solve for unknown force magnitudes and directions. These skills establish the mathematical competence required for advanced modules in work, energy, and momentum.
This course is a mandatory foundation for first-year university students of physics and engineering. It is equally beneficial for technical professionals needing a refresher on classical mechanics and pre-university students seeking a rigorous introduction to undergraduate dynamics. Mastery of these laws ensures a logical, structured approach to any scientific inquiry involving motion.
Force and Motion: Newton's Laws - Physics (Undergraduate Foundation)
Dynamics is the study of why objects move, and Newton's laws of motion provide the definitive mathematical framework for this analysis. This course transitions from kinematics to the rigorous application of force vectors, covering inertia, the quantitative relationship of mass and acceleration, and the necessity of action-reaction pairs. You will master the mechanics of special forces including gravity, tension, and springs, while resolving complex resistive interactions across static, kinetic, and fluid friction regimes. Every mechanical system - from civil engineering structures to aerospace propulsion - operates under these foundational principles. Understanding the interaction of forces is essential for predicting system failure, calculating vehicular safety margins, and designing efficient machinery. This knowledge provides the analytical tools required to solve real-world problems involving particle equilibrium and dynamic acceleration in both linear and circular paths. By the end of this course, you will be able to construct precise free-body diagrams to isolate bodies from their surroundings. You will acquire the technical skill to apply the second law to multi-force systems, calculate centripetal force requirements for uniform circular motion, and utilise the laws of equilibrium to solve for unknown force magnitudes and directions. These skills establish the mathematical competence required for advanced modules in work, energy, and momentum. This course is a mandatory foundation for first-year university students of physics and engineering. It is equally beneficial for technical professionals needing a refresher on classical mechanics and pre-university students seeking a rigorous introduction to undergraduate dynamics. Mastery of these laws ensures a logical, structured approach to any scientific inquiry involving motion.
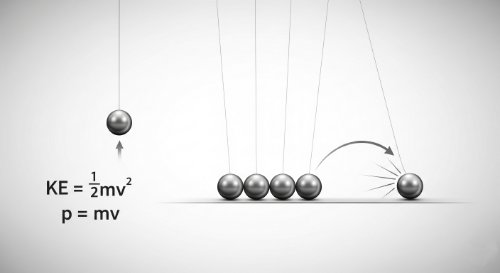
Work, Energy, and Momentum - Physics (Undergraduate Foundation)
This course provides an alternative, and often more efficient, approach to solving mechanics problems using the principles of work, energy, and momentum. It develops the work-energy theorem and the foundational laws of conservation of energy and conservation of linear momentum. These scalar (energy) and vector (momentum) methods are critical for analysing complex systems.
The conservation laws are among the most fundamental and powerful principles in all of science. They are applied in every field, from analysing planetary motion and particle collisions to understanding chemical reactions and engineering efficient machines. This course provides the mechanical foundation for these universal laws.
By the end of this course, you will be able to calculate the work done by a constant or variable force, apply the work-energy theorem to relate work and kinetic energy, solve problems using the principle of conservation of mechanical energy involving kinetic and potential energy, and apply the law of conservation of linear momentum to analyse collisions.
This course is a core requirement for all first-year university students of physics and engineering. It builds directly upon Newtonian dynamics and is the essential prerequisite for studying thermodynamics, fluid mechanics, and modern physics.
Work, Energy, and Momentum - Physics (Undergraduate Foundation)
This course provides an alternative, and often more efficient, approach to solving mechanics problems using the principles of work, energy, and momentum. It develops the work-energy theorem and the foundational laws of conservation of energy and conservation of linear momentum. These scalar (energy) and vector (momentum) methods are critical for analysing complex systems. The conservation laws are among the most fundamental and powerful principles in all of science. They are applied in every field, from analysing planetary motion and particle collisions to understanding chemical reactions and engineering efficient machines. This course provides the mechanical foundation for these universal laws. By the end of this course, you will be able to calculate the work done by a constant or variable force, apply the work-energy theorem to relate work and kinetic energy, solve problems using the principle of conservation of mechanical energy involving kinetic and potential energy, and apply the law of conservation of linear momentum to analyse collisions. This course is a core requirement for all first-year university students of physics and engineering. It builds directly upon Newtonian dynamics and is the essential prerequisite for studying thermodynamics, fluid mechanics, and modern physics.
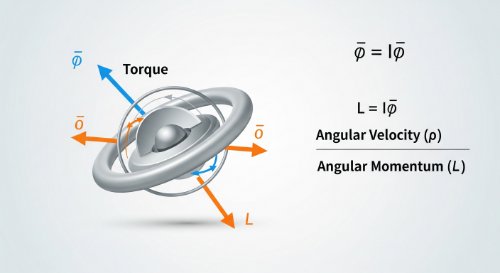
Rotational Motion and Angular Momentum - Physics (Undergraduate Foundation)
This course extends the principles of linear mechanics to rotational motion. It provides a complete analysis of the dynamics of rotating objects, covering the concepts of torque, angular momentum, and moment of inertia. Mastery of this material is essential for understanding any system that spins or orbits.
The principles of rotational dynamics are fundamental to engineering and physics. They are required to analyse the operation of engines, turbines, and gyroscopes, and to model the orbital mechanics of planets and satellites. This course provides the required analytical tools for these complex systems.
By the end of this course, you will be able to calculate torque for a given force, determine the moment of inertia for simple objects, apply the rotational equivalent of Newton's second law, and solve problems using the principle of conservation of angular momentum.
This course is designed for first-year university students of physics and engineering. It is a mandatory course that builds directly on Newtonian dynamics and is a prerequisite for studying planetary mechanics and rigid body dynamics.
Rotational Motion and Angular Momentum - Physics (Undergraduate Foundation)
This course extends the principles of linear mechanics to rotational motion. It provides a complete analysis of the dynamics of rotating objects, covering the concepts of torque, angular momentum, and moment of inertia. Mastery of this material is essential for understanding any system that spins or orbits. The principles of rotational dynamics are fundamental to engineering and physics. They are required to analyse the operation of engines, turbines, and gyroscopes, and to model the orbital mechanics of planets and satellites. This course provides the required analytical tools for these complex systems. By the end of this course, you will be able to calculate torque for a given force, determine the moment of inertia for simple objects, apply the rotational equivalent of Newton's second law, and solve problems using the principle of conservation of angular momentum. This course is designed for first-year university students of physics and engineering. It is a mandatory course that builds directly on Newtonian dynamics and is a prerequisite for studying planetary mechanics and rigid body dynamics.

Gravitation - Physics (Undergraduate Foundation)
This course provides a complete treatment of Newton's law of universal gravitation. It covers the principles governing the attractive force between masses, the concepts of gravitational fields and potential energy, and culminates in the application of these laws to the orbital mechanics of planets and satellites.
The law of gravitation is a fundamental principle of the cosmos. It is essential for understanding the motion of celestial bodies, launching and maintaining artificial satellites for communications and Earth observation, and for calculating interplanetary trajectories. This is the physics that governs the structure of the solar system and the universe.
By the end of this course, you will be able to apply Newton's law of universal gravitation to calculate the force between two masses, determine the gravitational potential energy of a system, explain Kepler's laws of planetary motion, and solve problems involving the orbital velocity and period of satellites.
This course is a mandatory part of the curriculum for first-year university students of physics and engineering. It directly builds upon the principles of rotational motion and dynamics and is a critical prerequisite for the study of astrophysics and celestial mechanics.
Gravitation - Physics (Undergraduate Foundation)
This course provides a complete treatment of Newton's law of universal gravitation. It covers the principles governing the attractive force between masses, the concepts of gravitational fields and potential energy, and culminates in the application of these laws to the orbital mechanics of planets and satellites. The law of gravitation is a fundamental principle of the cosmos. It is essential for understanding the motion of celestial bodies, launching and maintaining artificial satellites for communications and Earth observation, and for calculating interplanetary trajectories. This is the physics that governs the structure of the solar system and the universe. By the end of this course, you will be able to apply Newton's law of universal gravitation to calculate the force between two masses, determine the gravitational potential energy of a system, explain Kepler's laws of planetary motion, and solve problems involving the orbital velocity and period of satellites. This course is a mandatory part of the curriculum for first-year university students of physics and engineering. It directly builds upon the principles of rotational motion and dynamics and is a critical prerequisite for the study of astrophysics and celestial mechanics.