MTH 201: Mathematical Methods I
Learning Track Courses
 Functions and Their Graphs - Single-Variable Calculus (Undergraduate Foundation)This course provides a rigorous foundation in the concept of functions, the building block of calculus. We begin with the real number system - rationals, irrationals, intervals, and infinity - before defining real-valued functions, their domains, and ranges. You will systematically study all key function families: polynomial, rational, algebraic, piecewise-defined, and transcendental, including exponential, logarithmic, trigonometric, and hyperbolic types.
A command of functions is essential for all technical and quantitative disciplines. These principles are directly applied in physics to model motion, in economics for supply-demand curves, in engineering for signal processing, and in computer science to analyse algorithm complexity. This course delivers the core mathematical tools required for effective modelling and problem-solving in these fields and beyond.
By the end of this course, you will be able to: calculate the domain and range of any given function; classify functions and identify their fundamental properties; analyse functions for key characteristics like symmetry (odd and even); and accurately construct graphs for a wide range of standard and piecewise-defined functions directly from their equations.
This course is designed for first-year undergraduates in science, technology, engineering, mathematics (STEM), and economics. It is also critical for any student preparing for advanced calculus or for professionals who require a solid mathematical base for roles in finance, data science, or technical research.
Functions and Their Graphs - Single-Variable Calculus (Undergraduate Foundation)This course provides a rigorous foundation in the concept of functions, the building block of calculus. We begin with the real number system - rationals, irrationals, intervals, and infinity - before defining real-valued functions, their domains, and ranges. You will systematically study all key function families: polynomial, rational, algebraic, piecewise-defined, and transcendental, including exponential, logarithmic, trigonometric, and hyperbolic types.
A command of functions is essential for all technical and quantitative disciplines. These principles are directly applied in physics to model motion, in economics for supply-demand curves, in engineering for signal processing, and in computer science to analyse algorithm complexity. This course delivers the core mathematical tools required for effective modelling and problem-solving in these fields and beyond.
By the end of this course, you will be able to: calculate the domain and range of any given function; classify functions and identify their fundamental properties; analyse functions for key characteristics like symmetry (odd and even); and accurately construct graphs for a wide range of standard and piecewise-defined functions directly from their equations.
This course is designed for first-year undergraduates in science, technology, engineering, mathematics (STEM), and economics. It is also critical for any student preparing for advanced calculus or for professionals who require a solid mathematical base for roles in finance, data science, or technical research.
This course provides a rigorous foundation in the concept of functions, the building block of calculus. We begin with the real number system - rationals, irrationals, intervals, and infinity - before defining real-valued functions, their domains, and ranges. You will systematically study all key function families: polynomial, rational, algebraic, piecewise-defined, and transcendental, including exponential, logarithmic, trigonometric, and hyperbolic types. A command of functions is essential for all technical and quantitative disciplines. These principles are directly applied in physics to model motion, in economics for supply-demand curves, in engineering for signal processing, and in computer science to analyse algorithm complexity. This course delivers the core mathematical tools required for effective modelling and problem-solving in these fields and beyond. By the end of this course, you will be able to: calculate the domain and range of any given function; classify functions and identify their fundamental properties; analyse functions for key characteristics like symmetry (odd and even); and accurately construct graphs for a wide range of standard and piecewise-defined functions directly from their equations. This course is designed for first-year undergraduates in science, technology, engineering, mathematics (STEM), and economics. It is also critical for any student preparing for advanced calculus or for professionals who require a solid mathematical base for roles in finance, data science, or technical research.
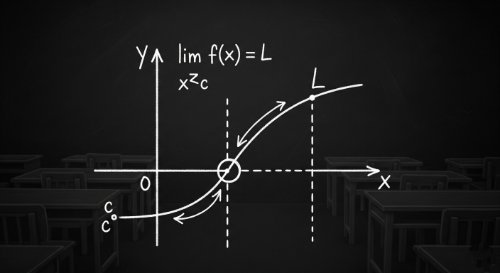 Limits of Functions - Single-Variable Calculus (Undergraduate Foundation)This course provides a rigorous introduction to the concept of the limit, the theoretical bedrock upon which all of calculus is built. We will move from an intuitive understanding of what it means for a function to 'approach' a value to the algebraic techniques required for precise evaluation. The course covers the limit laws, methods for handling indeterminate forms, and the behavior of functions at infinity.
Understanding limits is non-negotiable for any serious study of calculus. The principles developed here are not merely abstract; they are the tools used to formally define the core concepts of calculus that are used to model the mechanics of change that govern engineering, physics, economics, and computer science.
By the end of this course, you will be able to: evaluate limits graphically, numerically, and algebraically; apply the Squeeze Theorem and L’Hôpital’s Rule; analyse the end-behavior of functions; and identify vertical and horizontal asymptotes.
This course is designed for first-year undergraduates in STEM fields who are beginning their calculus sequence. It is an essential prerequisite for subsequent courses on continuity and differentiability and is also invaluable for any student or professional seeking to rebuild their mathematical foundation from first principles.
Limits of Functions - Single-Variable Calculus (Undergraduate Foundation)This course provides a rigorous introduction to the concept of the limit, the theoretical bedrock upon which all of calculus is built. We will move from an intuitive understanding of what it means for a function to 'approach' a value to the algebraic techniques required for precise evaluation. The course covers the limit laws, methods for handling indeterminate forms, and the behavior of functions at infinity.
Understanding limits is non-negotiable for any serious study of calculus. The principles developed here are not merely abstract; they are the tools used to formally define the core concepts of calculus that are used to model the mechanics of change that govern engineering, physics, economics, and computer science.
By the end of this course, you will be able to: evaluate limits graphically, numerically, and algebraically; apply the Squeeze Theorem and L’Hôpital’s Rule; analyse the end-behavior of functions; and identify vertical and horizontal asymptotes.
This course is designed for first-year undergraduates in STEM fields who are beginning their calculus sequence. It is an essential prerequisite for subsequent courses on continuity and differentiability and is also invaluable for any student or professional seeking to rebuild their mathematical foundation from first principles.
This course provides a rigorous introduction to the concept of the limit, the theoretical bedrock upon which all of calculus is built. We will move from an intuitive understanding of what it means for a function to 'approach' a value to the algebraic techniques required for precise evaluation. The course covers the limit laws, methods for handling indeterminate forms, and the behavior of functions at infinity. Understanding limits is non-negotiable for any serious study of calculus. The principles developed here are not merely abstract; they are the tools used to formally define the core concepts of calculus that are used to model the mechanics of change that govern engineering, physics, economics, and computer science. By the end of this course, you will be able to: evaluate limits graphically, numerically, and algebraically; apply the Squeeze Theorem and L’Hôpital’s Rule; analyse the end-behavior of functions; and identify vertical and horizontal asymptotes. This course is designed for first-year undergraduates in STEM fields who are beginning their calculus sequence. It is an essential prerequisite for subsequent courses on continuity and differentiability and is also invaluable for any student or professional seeking to rebuild their mathematical foundation from first principles.
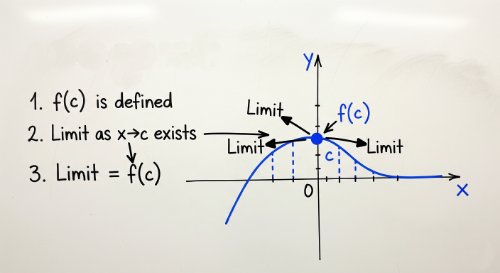 Continuity of Functions - Single-Variable Calculus (Undergraduate Foundation)This course provides a focused and rigorous examination of continuity, a fundamental property of functions that underpins the whole of differential and integral calculus. We move from an intuitive understanding of "unbroken" graphs to the formal, limit-based definition of continuity. The course systematically explores the different types of discontinuities and the powerful theorems that apply only to continuous functions.
A command of continuity is essential for understanding why calculus works. This concept ensures that functions are predictable and well-behaved, a necessary condition for modeling real-world phenomena and for the validity of the major theorems of calculus. It is the bridge between the concept of a limit and the concept of a derivative, explaining why a function must be continuous to be differentiable.
By the end of this course, you will be able to use the three-part definition to test for continuity at a point, identify and classify removable, jump, and infinite discontinuities, and apply the Intermediate Value Theorem and the Extreme Value Theorem to analyse function behavior on a closed interval.
This course is designed for first-year undergraduates in science, technology, engineering, and mathematics who have completed a course on limits. It is a critical prerequisite for the study of differentiability and is essential for any student seeking a deep understanding of calculus theory.
Continuity of Functions - Single-Variable Calculus (Undergraduate Foundation)This course provides a focused and rigorous examination of continuity, a fundamental property of functions that underpins the whole of differential and integral calculus. We move from an intuitive understanding of "unbroken" graphs to the formal, limit-based definition of continuity. The course systematically explores the different types of discontinuities and the powerful theorems that apply only to continuous functions.
A command of continuity is essential for understanding why calculus works. This concept ensures that functions are predictable and well-behaved, a necessary condition for modeling real-world phenomena and for the validity of the major theorems of calculus. It is the bridge between the concept of a limit and the concept of a derivative, explaining why a function must be continuous to be differentiable.
By the end of this course, you will be able to use the three-part definition to test for continuity at a point, identify and classify removable, jump, and infinite discontinuities, and apply the Intermediate Value Theorem and the Extreme Value Theorem to analyse function behavior on a closed interval.
This course is designed for first-year undergraduates in science, technology, engineering, and mathematics who have completed a course on limits. It is a critical prerequisite for the study of differentiability and is essential for any student seeking a deep understanding of calculus theory.
This course provides a focused and rigorous examination of continuity, a fundamental property of functions that underpins the whole of differential and integral calculus. We move from an intuitive understanding of "unbroken" graphs to the formal, limit-based definition of continuity. The course systematically explores the different types of discontinuities and the powerful theorems that apply only to continuous functions. A command of continuity is essential for understanding why calculus works. This concept ensures that functions are predictable and well-behaved, a necessary condition for modeling real-world phenomena and for the validity of the major theorems of calculus. It is the bridge between the concept of a limit and the concept of a derivative, explaining why a function must be continuous to be differentiable. By the end of this course, you will be able to use the three-part definition to test for continuity at a point, identify and classify removable, jump, and infinite discontinuities, and apply the Intermediate Value Theorem and the Extreme Value Theorem to analyse function behavior on a closed interval. This course is designed for first-year undergraduates in science, technology, engineering, and mathematics who have completed a course on limits. It is a critical prerequisite for the study of differentiability and is essential for any student seeking a deep understanding of calculus theory.
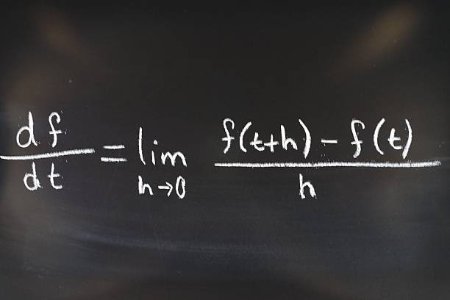 Differentiability of Functions - Single-Variable Calculus (Undergraduate Foundation)This course provides a rigorous, theoretical introduction to differential calculus. We will move beyond computation to understand the fundamental nature of the derivative, beginning with its formal definition as the limit of a difference quotient. The curriculum is designed to build a deep conceptual understanding of what it means for a function to be differentiable and the profound consequences of this property.
The primary focus is on formal proofs and theoretical results. We will systematically derive the rules of differentiation, including the product, quotient, and chain rules, directly from first principles. This course emphasizes the "why" behind the mechanics of calculus, establishing the logical framework upon which all applications are built, including the cornerstone theorems of Rolle, the Mean Value Theorem, and Taylor's Theorem.
By the end of this course, you will be able to: explain the derivative from its limit definition; prove the relationship between differentiability and continuity; formally derive all major differentiation rules; and understand the theoretical significance of the Mean Value Theorem and Taylor's Theorem.
This course is designed for first-year undergraduates in mathematics, physics, and engineering who require a deep theoretical foundation for their studies. It is the ideal precursor to subsequent courses on differentiation techniques and applications, providing the essential logical underpinnings for those more practical subjects.
Differentiability of Functions - Single-Variable Calculus (Undergraduate Foundation)This course provides a rigorous, theoretical introduction to differential calculus. We will move beyond computation to understand the fundamental nature of the derivative, beginning with its formal definition as the limit of a difference quotient. The curriculum is designed to build a deep conceptual understanding of what it means for a function to be differentiable and the profound consequences of this property.
The primary focus is on formal proofs and theoretical results. We will systematically derive the rules of differentiation, including the product, quotient, and chain rules, directly from first principles. This course emphasizes the "why" behind the mechanics of calculus, establishing the logical framework upon which all applications are built, including the cornerstone theorems of Rolle, the Mean Value Theorem, and Taylor's Theorem.
By the end of this course, you will be able to: explain the derivative from its limit definition; prove the relationship between differentiability and continuity; formally derive all major differentiation rules; and understand the theoretical significance of the Mean Value Theorem and Taylor's Theorem.
This course is designed for first-year undergraduates in mathematics, physics, and engineering who require a deep theoretical foundation for their studies. It is the ideal precursor to subsequent courses on differentiation techniques and applications, providing the essential logical underpinnings for those more practical subjects.
This course provides a rigorous, theoretical introduction to differential calculus. We will move beyond computation to understand the fundamental nature of the derivative, beginning with its formal definition as the limit of a difference quotient. The curriculum is designed to build a deep conceptual understanding of what it means for a function to be differentiable and the profound consequences of this property. The primary focus is on formal proofs and theoretical results. We will systematically derive the rules of differentiation, including the product, quotient, and chain rules, directly from first principles. This course emphasizes the "why" behind the mechanics of calculus, establishing the logical framework upon which all applications are built, including the cornerstone theorems of Rolle, the Mean Value Theorem, and Taylor's Theorem. By the end of this course, you will be able to: explain the derivative from its limit definition; prove the relationship between differentiability and continuity; formally derive all major differentiation rules; and understand the theoretical significance of the Mean Value Theorem and Taylor's Theorem. This course is designed for first-year undergraduates in mathematics, physics, and engineering who require a deep theoretical foundation for their studies. It is the ideal precursor to subsequent courses on differentiation techniques and applications, providing the essential logical underpinnings for those more practical subjects.
 Convergence of Infinite Sequences and Series - Advanced Calculus (Undergraduate Advanced)This course provides a complete toolkit for the study of infinite sequences and series. It begins with a rigorous treatment of the convergence of sequences and the algebra of limits. The course then covers the foundational theory of infinite series and provides a comprehensive study of all standard tests for convergence, culminating in an introduction to power series.
The concepts of convergence and infinite series are essential in physics, engineering, and computer science. They are used to solve differential equations, analyse signals with Fourier series, calculate probabilities, and determine the accuracy of numerical approximations. This is the mathematical machinery behind precision in scientific modelling.
By the end of this course, you will be able to determine if an infinite sequence converges and find its limit. You will also be able to apply the complete suite of convergence tests—including the Integral, Comparison, Ratio, Root, and Alternating Series tests—to determine if an infinite series converges, and find the radius and interval of convergence for any power series.
This course is for students who have completed a foundational calculus course. It is the standard curriculum for a second-semester calculus (Calculus II) module and is a direct prerequisite for the study of differential equations, complex analysis, and advanced physics.
Convergence of Infinite Sequences and Series - Advanced Calculus (Undergraduate Advanced)This course provides a complete toolkit for the study of infinite sequences and series. It begins with a rigorous treatment of the convergence of sequences and the algebra of limits. The course then covers the foundational theory of infinite series and provides a comprehensive study of all standard tests for convergence, culminating in an introduction to power series.
The concepts of convergence and infinite series are essential in physics, engineering, and computer science. They are used to solve differential equations, analyse signals with Fourier series, calculate probabilities, and determine the accuracy of numerical approximations. This is the mathematical machinery behind precision in scientific modelling.
By the end of this course, you will be able to determine if an infinite sequence converges and find its limit. You will also be able to apply the complete suite of convergence tests—including the Integral, Comparison, Ratio, Root, and Alternating Series tests—to determine if an infinite series converges, and find the radius and interval of convergence for any power series.
This course is for students who have completed a foundational calculus course. It is the standard curriculum for a second-semester calculus (Calculus II) module and is a direct prerequisite for the study of differential equations, complex analysis, and advanced physics.
This course provides a complete toolkit for the study of infinite sequences and series. It begins with a rigorous treatment of the convergence of sequences and the algebra of limits. The course then covers the foundational theory of infinite series and provides a comprehensive study of all standard tests for convergence, culminating in an introduction to power series. The concepts of convergence and infinite series are essential in physics, engineering, and computer science. They are used to solve differential equations, analyse signals with Fourier series, calculate probabilities, and determine the accuracy of numerical approximations. This is the mathematical machinery behind precision in scientific modelling. By the end of this course, you will be able to determine if an infinite sequence converges and find its limit. You will also be able to apply the complete suite of convergence tests—including the Integral, Comparison, Ratio, Root, and Alternating Series tests—to determine if an infinite series converges, and find the radius and interval of convergence for any power series. This course is for students who have completed a foundational calculus course. It is the standard curriculum for a second-semester calculus (Calculus II) module and is a direct prerequisite for the study of differential equations, complex analysis, and advanced physics.
 Analysis of Infinite Sequences and Series - Real Analysis (Undergraduate Advanced)This course provides the formal, proof-based foundation for the concepts of convergence covered in calculus. It moves beyond computation to explore the deep theoretical questions of why sequences and series converge. The material covers the topological properties of sequences, key convergence theorems like Bolzano-Weierstrass, Cauchy sequences, and the advanced topic of uniform convergence for series of functions.
This subject is the gateway to higher mathematics. The rigorous proof-writing and analytical skills developed here are non-negotiable for any student pursuing a degree in pure or applied mathematics. These principles are the theoretical bedrock upon which advanced concepts in differential equations, functional analysis, and theoretical physics are built.
By the end of this course, you will be able to construct rigorous proofs for statements about the convergence of sequences. You will also be able to apply the Monotone Convergence and Bolzano-Weierstrass theorems, use the Cauchy Criterion to prove convergence, and analyse the uniform convergence of a series of functions using the Weierstrass M-Test.
This course is for mathematics majors and advanced students who have already completed a full Calculus II course. It is the standard curriculum for a first module in Real Analysis and is an essential prerequisite for graduate-level study in mathematics, physics, and theoretical computer science.
Analysis of Infinite Sequences and Series - Real Analysis (Undergraduate Advanced)This course provides the formal, proof-based foundation for the concepts of convergence covered in calculus. It moves beyond computation to explore the deep theoretical questions of why sequences and series converge. The material covers the topological properties of sequences, key convergence theorems like Bolzano-Weierstrass, Cauchy sequences, and the advanced topic of uniform convergence for series of functions.
This subject is the gateway to higher mathematics. The rigorous proof-writing and analytical skills developed here are non-negotiable for any student pursuing a degree in pure or applied mathematics. These principles are the theoretical bedrock upon which advanced concepts in differential equations, functional analysis, and theoretical physics are built.
By the end of this course, you will be able to construct rigorous proofs for statements about the convergence of sequences. You will also be able to apply the Monotone Convergence and Bolzano-Weierstrass theorems, use the Cauchy Criterion to prove convergence, and analyse the uniform convergence of a series of functions using the Weierstrass M-Test.
This course is for mathematics majors and advanced students who have already completed a full Calculus II course. It is the standard curriculum for a first module in Real Analysis and is an essential prerequisite for graduate-level study in mathematics, physics, and theoretical computer science.
This course provides the formal, proof-based foundation for the concepts of convergence covered in calculus. It moves beyond computation to explore the deep theoretical questions of why sequences and series converge. The material covers the topological properties of sequences, key convergence theorems like Bolzano-Weierstrass, Cauchy sequences, and the advanced topic of uniform convergence for series of functions. This subject is the gateway to higher mathematics. The rigorous proof-writing and analytical skills developed here are non-negotiable for any student pursuing a degree in pure or applied mathematics. These principles are the theoretical bedrock upon which advanced concepts in differential equations, functional analysis, and theoretical physics are built. By the end of this course, you will be able to construct rigorous proofs for statements about the convergence of sequences. You will also be able to apply the Monotone Convergence and Bolzano-Weierstrass theorems, use the Cauchy Criterion to prove convergence, and analyse the uniform convergence of a series of functions using the Weierstrass M-Test. This course is for mathematics majors and advanced students who have already completed a full Calculus II course. It is the standard curriculum for a first module in Real Analysis and is an essential prerequisite for graduate-level study in mathematics, physics, and theoretical computer science.
 Partial Differentiation and Its Applications - Multivariable Calculus (Undergraduate Advanced)This course provides a complete guide to the calculus of several variables. It builds from the foundational concepts of multivariable functions, limits, and continuity to the core techniques of differentiation, including partial derivatives, the chain rule, and implicit differentiation. The material culminates in advanced topics such as Taylor's theorem for several variables and the use of Jacobians.
Multivariable calculus is the language of modern science, engineering, and economics. Its principles are used to model complex surfaces, analyse thermodynamic systems, create 3D computer graphics, and solve critical optimisation problems in business and finance. This is the mathematical toolkit for working with systems that have multiple interacting variables.
By the end of this course, you will be able to calculate partial derivatives, apply the multivariable chain rule, and find directional derivatives using the gradient vector. You will also be able to solve both unconstrained and constrained optimisation problems by finding extreme values and using the method of Lagrange multipliers, and apply these derivatives to find tangent planes to surfaces.
This course is for students who have completed a full single-variable calculus sequence. It is the standard curriculum for a multivariable calculus (Calculus III) module and is a direct prerequisite for the study of vector calculus, differential equations, and advanced courses in physics, engineering, and economics.
Partial Differentiation and Its Applications - Multivariable Calculus (Undergraduate Advanced)This course provides a complete guide to the calculus of several variables. It builds from the foundational concepts of multivariable functions, limits, and continuity to the core techniques of differentiation, including partial derivatives, the chain rule, and implicit differentiation. The material culminates in advanced topics such as Taylor's theorem for several variables and the use of Jacobians.
Multivariable calculus is the language of modern science, engineering, and economics. Its principles are used to model complex surfaces, analyse thermodynamic systems, create 3D computer graphics, and solve critical optimisation problems in business and finance. This is the mathematical toolkit for working with systems that have multiple interacting variables.
By the end of this course, you will be able to calculate partial derivatives, apply the multivariable chain rule, and find directional derivatives using the gradient vector. You will also be able to solve both unconstrained and constrained optimisation problems by finding extreme values and using the method of Lagrange multipliers, and apply these derivatives to find tangent planes to surfaces.
This course is for students who have completed a full single-variable calculus sequence. It is the standard curriculum for a multivariable calculus (Calculus III) module and is a direct prerequisite for the study of vector calculus, differential equations, and advanced courses in physics, engineering, and economics.
This course provides a complete guide to the calculus of several variables. It builds from the foundational concepts of multivariable functions, limits, and continuity to the core techniques of differentiation, including partial derivatives, the chain rule, and implicit differentiation. The material culminates in advanced topics such as Taylor's theorem for several variables and the use of Jacobians. Multivariable calculus is the language of modern science, engineering, and economics. Its principles are used to model complex surfaces, analyse thermodynamic systems, create 3D computer graphics, and solve critical optimisation problems in business and finance. This is the mathematical toolkit for working with systems that have multiple interacting variables. By the end of this course, you will be able to calculate partial derivatives, apply the multivariable chain rule, and find directional derivatives using the gradient vector. You will also be able to solve both unconstrained and constrained optimisation problems by finding extreme values and using the method of Lagrange multipliers, and apply these derivatives to find tangent planes to surfaces. This course is for students who have completed a full single-variable calculus sequence. It is the standard curriculum for a multivariable calculus (Calculus III) module and is a direct prerequisite for the study of vector calculus, differential equations, and advanced courses in physics, engineering, and economics.
 Introduction to Numerical Methods (Undergraduate Foundation)This course covers numerical methods for solving problems that have no exact analytical solution. It is a practical study of iterative approximation techniques. The material is focused on two core areas: finding the roots of single-variable equations using the Bisection and Newton's methods, and approximating definite integrals using the Trapezoidal and Simpson's rules.
Numerical methods are the foundation of all modern computational problem-solving in science, engineering, and finance. These are the algorithms that power computer simulations, engineering design software, and financial modelling tools. The ability to find approximate solutions to complex equations is a fundamental skill for any technical or scientific professional.
By the end of this course, you will be able to apply the Bisection and Newton's methods to find the roots of single-variable equations. You will also be able to use the Trapezoidal and Simpson's rules to calculate the approximate value of definite integrals, providing a core toolkit for numerical approximation.
This course is for undergraduate foundation students in engineering, physics, and computer science. It is an essential topic for anyone who will use computational tools to solve mathematical problems. A solid understanding of single-variable calculus is a prerequisite.
Introduction to Numerical Methods (Undergraduate Foundation)This course covers numerical methods for solving problems that have no exact analytical solution. It is a practical study of iterative approximation techniques. The material is focused on two core areas: finding the roots of single-variable equations using the Bisection and Newton's methods, and approximating definite integrals using the Trapezoidal and Simpson's rules.
Numerical methods are the foundation of all modern computational problem-solving in science, engineering, and finance. These are the algorithms that power computer simulations, engineering design software, and financial modelling tools. The ability to find approximate solutions to complex equations is a fundamental skill for any technical or scientific professional.
By the end of this course, you will be able to apply the Bisection and Newton's methods to find the roots of single-variable equations. You will also be able to use the Trapezoidal and Simpson's rules to calculate the approximate value of definite integrals, providing a core toolkit for numerical approximation.
This course is for undergraduate foundation students in engineering, physics, and computer science. It is an essential topic for anyone who will use computational tools to solve mathematical problems. A solid understanding of single-variable calculus is a prerequisite.
This course covers numerical methods for solving problems that have no exact analytical solution. It is a practical study of iterative approximation techniques. The material is focused on two core areas: finding the roots of single-variable equations using the Bisection and Newton's methods, and approximating definite integrals using the Trapezoidal and Simpson's rules. Numerical methods are the foundation of all modern computational problem-solving in science, engineering, and finance. These are the algorithms that power computer simulations, engineering design software, and financial modelling tools. The ability to find approximate solutions to complex equations is a fundamental skill for any technical or scientific professional. By the end of this course, you will be able to apply the Bisection and Newton's methods to find the roots of single-variable equations. You will also be able to use the Trapezoidal and Simpson's rules to calculate the approximate value of definite integrals, providing a core toolkit for numerical approximation. This course is for undergraduate foundation students in engineering, physics, and computer science. It is an essential topic for anyone who will use computational tools to solve mathematical problems. A solid understanding of single-variable calculus is a prerequisite.
 Ordinary Differential Equations - Mathematical Methods (Undergraduate Advanced)This course provides a complete guide to solving ordinary differential equations (ODEs). It covers the classification of differential equations and details the solution methods for first-order equations, including separable, homogeneous, exact, and linear types. The course then moves to second-order linear equations with constant coefficients and covers the methods of undetermined coefficients and variation of parameters.
Differential equations are the mathematical language used to model dynamic systems in science and engineering. They are used to describe the motion of objects, the flow of electric circuits, population growth, radioactive decay, and chemical reaction rates. A command of this subject is a non-negotiable requirement for any serious study in physics, engineering, or applied mathematics.
By the end of this course, you will be able to classify any ordinary differential equation by its order, degree, and linearity. You will be able to solve a wide variety of first-order ODEs and constant-coefficient second-order ODEs. You will also be able to model and solve real-world problems, such as orthogonal trajectories, exponential growth and decay, and simple electric circuits.
This course is for undergraduate students in mathematics, physics, engineering, and chemistry. It is a standard module in any mathematical methods curriculum and assumes a full prerequisite knowledge of single and multivariable calculus. It is an essential foundation for the study of partial differential equations, control theory, and advanced physics.
Ordinary Differential Equations - Mathematical Methods (Undergraduate Advanced)This course provides a complete guide to solving ordinary differential equations (ODEs). It covers the classification of differential equations and details the solution methods for first-order equations, including separable, homogeneous, exact, and linear types. The course then moves to second-order linear equations with constant coefficients and covers the methods of undetermined coefficients and variation of parameters.
Differential equations are the mathematical language used to model dynamic systems in science and engineering. They are used to describe the motion of objects, the flow of electric circuits, population growth, radioactive decay, and chemical reaction rates. A command of this subject is a non-negotiable requirement for any serious study in physics, engineering, or applied mathematics.
By the end of this course, you will be able to classify any ordinary differential equation by its order, degree, and linearity. You will be able to solve a wide variety of first-order ODEs and constant-coefficient second-order ODEs. You will also be able to model and solve real-world problems, such as orthogonal trajectories, exponential growth and decay, and simple electric circuits.
This course is for undergraduate students in mathematics, physics, engineering, and chemistry. It is a standard module in any mathematical methods curriculum and assumes a full prerequisite knowledge of single and multivariable calculus. It is an essential foundation for the study of partial differential equations, control theory, and advanced physics.
This course provides a complete guide to solving ordinary differential equations (ODEs). It covers the classification of differential equations and details the solution methods for first-order equations, including separable, homogeneous, exact, and linear types. The course then moves to second-order linear equations with constant coefficients and covers the methods of undetermined coefficients and variation of parameters. Differential equations are the mathematical language used to model dynamic systems in science and engineering. They are used to describe the motion of objects, the flow of electric circuits, population growth, radioactive decay, and chemical reaction rates. A command of this subject is a non-negotiable requirement for any serious study in physics, engineering, or applied mathematics. By the end of this course, you will be able to classify any ordinary differential equation by its order, degree, and linearity. You will be able to solve a wide variety of first-order ODEs and constant-coefficient second-order ODEs. You will also be able to model and solve real-world problems, such as orthogonal trajectories, exponential growth and decay, and simple electric circuits. This course is for undergraduate students in mathematics, physics, engineering, and chemistry. It is a standard module in any mathematical methods curriculum and assumes a full prerequisite knowledge of single and multivariable calculus. It is an essential foundation for the study of partial differential equations, control theory, and advanced physics.