MTH 207: Real Analysis I
Learning Track Courses
Convergence of Infinite Sequences and Series - Advanced Calculus (Undergraduate Advanced)
This course provides a complete toolkit for the study of infinite sequences and series. It begins with a rigorous treatment of the convergence of sequences and the algebra of limits. The course then covers the foundational theory of infinite series and provides a comprehensive study of all standard tests for convergence, culminating in an introduction to power series.
The concepts of convergence and infinite series are essential in physics, engineering, and computer science. They are used to solve differential equations, analyse signals with Fourier series, calculate probabilities, and determine the accuracy of numerical approximations. This is the mathematical machinery behind precision in scientific modelling.
By the end of this course, you will be able to determine if an infinite sequence converges and find its limit. You will also be able to apply the complete suite of convergence tests???including the Integral, Comparison, Ratio, Root, and Alternating Series tests???to determine if an infinite series converges, and find the radius and interval of convergence for any power series.
This course is for students who have completed a foundational calculus course. It is the standard curriculum for a second-semester calculus (Calculus II) module and is a direct prerequisite for the study of differential equations, complex analysis, and advanced physics.
Convergence of Infinite Sequences and Series - Advanced Calculus (Undergraduate Advanced)
This course provides a complete toolkit for the study of infinite sequences and series. It begins with a rigorous treatment of the convergence of sequences and the algebra of limits. The course then covers the foundational theory of infinite series and provides a comprehensive study of all standard tests for convergence, culminating in an introduction to power series. The concepts of convergence and infinite series are essential in physics, engineering, and computer science. They are used to solve differential equations, analyse signals with Fourier series, calculate probabilities, and determine the accuracy of numerical approximations. This is the mathematical machinery behind precision in scientific modelling. By the end of this course, you will be able to determine if an infinite sequence converges and find its limit. You will also be able to apply the complete suite of convergence tests???including the Integral, Comparison, Ratio, Root, and Alternating Series tests???to determine if an infinite series converges, and find the radius and interval of convergence for any power series. This course is for students who have completed a foundational calculus course. It is the standard curriculum for a second-semester calculus (Calculus II) module and is a direct prerequisite for the study of differential equations, complex analysis, and advanced physics.
Analysis of Infinite Sequences and Series - Real Analysis (Undergraduate Advanced)
This course provides the formal, proof-based foundation for the concepts of convergence covered in calculus. It moves beyond computation to explore the deep theoretical questions of why sequences and series converge. The material covers the topological properties of sequences, key convergence theorems like Bolzano-Weierstrass, Cauchy sequences, and the advanced topic of uniform convergence for series of functions.
This subject is the gateway to higher mathematics. The rigorous proof-writing and analytical skills developed here are non-negotiable for any student pursuing a degree in pure or applied mathematics. These principles are the theoretical bedrock upon which advanced concepts in differential equations, functional analysis, and theoretical physics are built.
By the end of this course, you will be able to construct rigorous proofs for statements about the convergence of sequences. You will also be able to apply the Monotone Convergence and Bolzano-Weierstrass theorems, use the Cauchy Criterion to prove convergence, and analyse the uniform convergence of a series of functions using the Weierstrass M-Test.
This course is for mathematics majors and advanced students who have already completed a full Calculus II course. It is the standard curriculum for a first module in Real Analysis and is an essential prerequisite for graduate-level study in mathematics, physics, and theoretical computer science.
Analysis of Infinite Sequences and Series - Real Analysis (Undergraduate Advanced)
This course provides the formal, proof-based foundation for the concepts of convergence covered in calculus. It moves beyond computation to explore the deep theoretical questions of why sequences and series converge. The material covers the topological properties of sequences, key convergence theorems like Bolzano-Weierstrass, Cauchy sequences, and the advanced topic of uniform convergence for series of functions. This subject is the gateway to higher mathematics. The rigorous proof-writing and analytical skills developed here are non-negotiable for any student pursuing a degree in pure or applied mathematics. These principles are the theoretical bedrock upon which advanced concepts in differential equations, functional analysis, and theoretical physics are built. By the end of this course, you will be able to construct rigorous proofs for statements about the convergence of sequences. You will also be able to apply the Monotone Convergence and Bolzano-Weierstrass theorems, use the Cauchy Criterion to prove convergence, and analyse the uniform convergence of a series of functions using the Weierstrass M-Test. This course is for mathematics majors and advanced students who have already completed a full Calculus II course. It is the standard curriculum for a first module in Real Analysis and is an essential prerequisite for graduate-level study in mathematics, physics, and theoretical computer science.
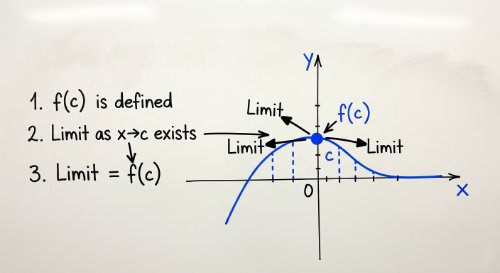
Continuity of Functions - Single-Variable Calculus (Undergraduate Foundation)
This course provides a focused and rigorous examination of continuity, a fundamental property of functions that underpins the whole of differential and integral calculus. We move from an intuitive understanding of "unbroken" graphs to the formal, limit-based definition of continuity. The course systematically explores the different types of discontinuities and the powerful theorems that apply only to continuous functions.
A command of continuity is essential for understanding why calculus works. This concept ensures that functions are predictable and well-behaved, a necessary condition for modeling real-world phenomena and for the validity of the major theorems of calculus. It is the bridge between the concept of a limit and the concept of a derivative, explaining why a function must be continuous to be differentiable.
By the end of this course, you will be able to use the three-part definition to test for continuity at a point, identify and classify removable, jump, and infinite discontinuities, and apply the Intermediate Value Theorem and the Extreme Value Theorem to analyse function behavior on a closed interval.
This course is designed for first-year undergraduates in science, technology, engineering, and mathematics who have completed a course on limits. It is a critical prerequisite for the study of differentiability and is essential for any student seeking a deep understanding of calculus theory.
Continuity of Functions - Single-Variable Calculus (Undergraduate Foundation)
This course provides a focused and rigorous examination of continuity, a fundamental property of functions that underpins the whole of differential and integral calculus. We move from an intuitive understanding of "unbroken" graphs to the formal, limit-based definition of continuity. The course systematically explores the different types of discontinuities and the powerful theorems that apply only to continuous functions. A command of continuity is essential for understanding why calculus works. This concept ensures that functions are predictable and well-behaved, a necessary condition for modeling real-world phenomena and for the validity of the major theorems of calculus. It is the bridge between the concept of a limit and the concept of a derivative, explaining why a function must be continuous to be differentiable. By the end of this course, you will be able to use the three-part definition to test for continuity at a point, identify and classify removable, jump, and infinite discontinuities, and apply the Intermediate Value Theorem and the Extreme Value Theorem to analyse function behavior on a closed interval. This course is designed for first-year undergraduates in science, technology, engineering, and mathematics who have completed a course on limits. It is a critical prerequisite for the study of differentiability and is essential for any student seeking a deep understanding of calculus theory.
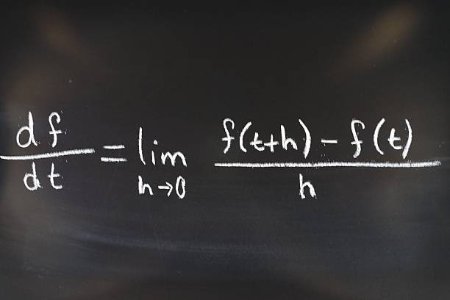
Differentiability of Functions - Single-Variable Calculus (Undergraduate Foundation)
This course provides a rigorous, theoretical introduction to differential calculus. We will move beyond computation to understand the fundamental nature of the derivative, beginning with its formal definition as the limit of a difference quotient. The curriculum is designed to build a deep conceptual understanding of what it means for a function to be differentiable and the profound consequences of this property.
The primary focus is on formal proofs and theoretical results. We will systematically derive the rules of differentiation, including the product, quotient, and chain rules, directly from first principles. This course emphasizes the "why" behind the mechanics of calculus, establishing the logical framework upon which all applications are built, including the cornerstone theorems of Rolle, the Mean Value Theorem, and Taylor's Theorem.
By the end of this course, you will be able to: explain the derivative from its limit definition; prove the relationship between differentiability and continuity; formally derive all major differentiation rules; and understand the theoretical significance of the Mean Value Theorem and Taylor's Theorem.
This course is designed for first-year undergraduates in mathematics, physics, and engineering who require a deep theoretical foundation for their studies. It is the ideal precursor to subsequent courses on differentiation techniques and applications, providing the essential logical underpinnings for those more practical subjects.
Differentiability of Functions - Single-Variable Calculus (Undergraduate Foundation)
This course provides a rigorous, theoretical introduction to differential calculus. We will move beyond computation to understand the fundamental nature of the derivative, beginning with its formal definition as the limit of a difference quotient. The curriculum is designed to build a deep conceptual understanding of what it means for a function to be differentiable and the profound consequences of this property. The primary focus is on formal proofs and theoretical results. We will systematically derive the rules of differentiation, including the product, quotient, and chain rules, directly from first principles. This course emphasizes the "why" behind the mechanics of calculus, establishing the logical framework upon which all applications are built, including the cornerstone theorems of Rolle, the Mean Value Theorem, and Taylor's Theorem. By the end of this course, you will be able to: explain the derivative from its limit definition; prove the relationship between differentiability and continuity; formally derive all major differentiation rules; and understand the theoretical significance of the Mean Value Theorem and Taylor's Theorem. This course is designed for first-year undergraduates in mathematics, physics, and engineering who require a deep theoretical foundation for their studies. It is the ideal precursor to subsequent courses on differentiation techniques and applications, providing the essential logical underpinnings for those more practical subjects.